Introduce
我們這次要介紹決策樹,決策樹其實對人類來說是最直覺最直觀的方法,我們來考慮一個情境題, 假設媽媽要你幫她去買文具,你開始思考如果外面天氣不好下雨或是太陽太大就在家休息, 然後你看到天氣不錯的那一天,你覺得自己一個人去買文具太無聊要拉個朋友,如果小美、小萌、小慧誰有空陪你去你就願意出門, 然後開始打電話,你約到小萌有空陪你去,到了賣場挑完原子筆、膠水、筆記本、釘書機等文具,你發現香水、指甲油等等你都想要買, 你發現蛙阿錢包裡的錢不夠,你跟小萌說我帶的錢不夠可以借我一點錢嗎? 小萌說不行這些她的錢要拿來裝可愛買娃娃的,你只好回家找媽媽要錢,媽媽就問你說你到底是怎麼做事的, 交辦這麼多天東西還沒買好,去做一份流程圖再來拿錢,你就把你的策略寫下來。
於是你畫下你的決策樹。
手繪決策樹
/images/consume.drawio.png)決策樹的想法是不是很直接與直觀,下面我們來看 Iris 資料集的決策樹的圖。
from sklearn.tree import plot_tree
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = [10, 10]
iris = load_iris()
classifier = DecisionTreeClassifier().fit(iris.data, iris.target)
plt.figure()
plot_tree(classifier, filled=True)
plt.title("Decision tree trained on all the iris features")
plt.show()
下面來簡單驗證看看。
# 驗證看看
iris.target[iris.data[:,2] < 2.45]
如果換個參數,用 entropy。
from sklearn.tree import plot_tree
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['figure.figsize'] = [10, 10]
iris = load_iris()
classifier = DecisionTreeClassifier(criterion='entropy').fit(iris.data, iris.target)
plt.figure()
plot_tree(classifier, filled=True)
plt.title("Decision tree trained on all the iris features")
plt.show()
from scipy.stats import entropy
entropy([1], base=2)
#entropy([1/2, 1/2], base=2)
#entropy([1/3, 1/3, 1/3], base=2)
# ??DecisionTreeClassifier
決策樹在機器學習的方法裡面算是最直觀的方法,看完上面的例子,我猜大家會有的問題是那我要如何決定分支,所以下面要介紹 information theory。
Information theory
我們下面來說一下 1948 年 , Claude Shannon 提出的 information theory 是怎麼理解的,下面我們看一張圖。
/images/gini_entropy.drawio.png)
請問你覺得哪個最亂? 哪個資訊比較多?
如果給定隨機變數 $X$ , $P$ 為 $X$ 的機率密度函數 Probability Density Function , 下面要介紹怎麼衡量一組資訊的混亂程度,常見的有三種 Entropy、Gini impurity、Classification Error。
Entropy、Gini、C.E. 範例
## Entropy 熵 $$ I_H(X) := - \sum_{i=1}^n P(x_i) \log_2 P(x_i) $$ - 圖(A)的 Entropy 是 0 - 圖(B)的 Entropy 是 1 $$ -(\frac{\log_2 (1/2)}{2} + \frac{\log_2 (1/2)}{2}) = -\log_2 (1/2) = 1 $$ - 圖(C)的 Entropy 是 1.585 $$ -(\frac{\log_2 (1/3)}{3} * 3) = -\log_2 (1/3) \sim 1.585 $$ ## Gini impurity 不純度 $$ I_G(X) := 1 - \sum_{i=1}^n P(x_i)^2 $$ - 圖(A)的 Gini impurity 是 0 - 圖(B)的 Gini impurity 是 $\frac{1}{2}$ $$ 1 - (\frac{1}{2^2} + \frac{1}{2^2}) = 1 - \frac{1}{2} = \frac{1}{2} $$ - 圖(C)的 Gini impurity 是 $\frac{2}{3}$ $$ 1 - \frac{1}{3^2} * 3 = 1 - \frac{1}{3} = \frac{2}{3} $$ ## Classification Error $$ I_E(X) := 1 - \max \{ P(x_i) \} $$ - 圖(A)的 Classification Error 是 0 - 圖(B)的 Classification Error 是 $\frac{1}{2}$ - 圖(C)的 Classification Error 是 $\frac{2}{3}$衡量財富不均的吉尼係數 Gini coefficient
是 20 世紀初,義大利統計學家 Corrado Gini 提出的 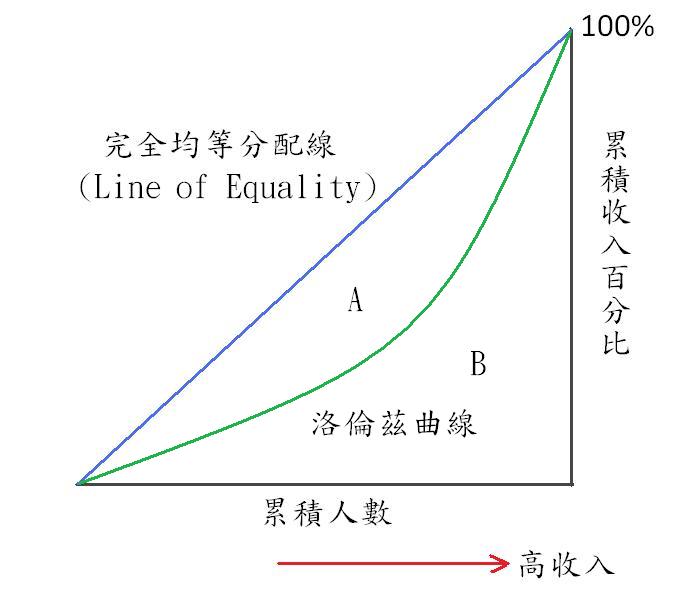 $$ \frac{A}{A+B} = 1 - \frac{B}{A+B} $$ Gini coefficient 是介於 0 到 1 之間的值,0 表示大家的收入完全一樣 - 若低於 $0.2$ 表示 財富很平均 - $0.2 \sim 0.29$ 表示 **財富不均** 低; - $0.3 \sim 0.39$ 表示 **財富不均** 中等; - $0.4 \sim 0.59$ 表示 **財富不均** 高; - $0.6$ 以上表示 **財富不均** 極高。 我們回到我們的例子,假設藍色是收入100,紅色是收入0,綠色是收入50。 - 圖(A)的 吉尼係數是 0 - 圖(B)的 吉尼係數是 1/2 - 圖(C)的 吉尼係數是 1/3 我們可以知道跟 information theory 提到的有一些差別, 很明顯的一點根據定義給不同顏色不同收入,吉尼係數是不一樣的, 但是對於 information theory 來說是一樣的。下面要談談 信息增益
信息增益 Information Gain (IG)
\[IG(X) := I(X) - \frac{N_{left}}{N} I(X_{left}) - \frac{N_{right}}{N} I(X_{right})\]我們以上面為例計算信息增益,我們的策略是要讓分支,使得信息增益越大越好。
Example
50 50 50 --> 50 0 0 --> 0 50 50 ### Entropy $$ I_H(X) \sim 1.585 $$ $$ I_H(X_{left}) = 0 $$ $$ I_H(X_{right}) = 1 $$ $$ I_H(X) - \frac{N_{left}}{N} I_H(X_{left}) - \frac{N_{right}}{N} I_H(X_{right}) \sim 1.585 - \frac{50}{150} * 0 - \frac{100}{150} * 1 \sim 0.919 $$ ### Gini impurity $$ I_G(X) = \frac{2}{3} $$ $$ I_G(X_{left}) = 0 $$ $$ I_G(X_{right}) = \frac{1}{2} $$ $$ I_G(X) - \frac{N_{left}}{N} I_G(X_{left}) - \frac{N_{right}}{N} I_G(X_{right}) = \frac{2}{3} - \frac{50}{150} * 0 - \frac{100}{150} * \frac{1}{2} = \frac{1}{3} $$ ### Classification Error $$ I_E(X) = \frac{2}{3} $$ $$ I_E(X_{left}) = 0 $$ $$ I_E(X_{right}) = \frac{1}{2} $$ $$ I_E(X) - \frac{N_{left}}{N} I_E(X_{left}) - \frac{N_{right}}{N} I_E(X_{right}) = \frac{2}{3} - \frac{50}{150} * 0 - \frac{100}{150} * \frac{1}{2} = \frac{1}{3} $$ID3
ID3 的演算法在決定決策樹上各子節點根據 信息增益 去計算所有可能的特徵, 選 信息增益 最大的特徵作為節點特徵,但是 ID3 有一個缺點就是如果是有多值屬性的變量會影響很大, 例如 唯一屬性,你的身分證號碼,或是 UUID。
C4.5
C4.5 是 ID3 的改進版
- 用信息增益比來選屬性 (可以解決多值屬性敏感問題)
- 對非離散數據也能處理 (用 if-then 規則集來處理)
- 能夠處理數據缺失
C5.0
C5.0 改進了
- 速度更快
- 更高效的内存使用
CART
CART 與 C4.5 算法是非常相似的,但是CART支持預測連續的值。
| 多值屬性 | 能否處理缺失職 | 處理數據類形 | |
|---|---|---|---|
| ID3 | 敏感 | 不能 | 離散 |
| C4.5 | 不敏感 | 可以 | 離散、連續 |
| C5.0 | 不敏感 | 可以 | 離散、連續 |
| CART | 不敏感 | 可以 | 離散、連續 |
scikit-learn 使用 CART 算法的優化版本,但是 scikit-learn 目前還不支持分類變量。